-
그리디&구현, DFS&BFSAlgorithm 2020. 9. 1. 21:52
그리디 & 구현
- 시각
import java.io.*; public class Main { public static void main(String[] args) throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); /** * 구현 * 시각 * N시 59분 59초까지 3이 하나라도 포함되는 모든 경우의 수 */ int h = Integer.parseInt(br.readLine()); int cnt = 0; for (int i = 0; i <= h; i++) { for (int j = 0; j < 60; j++) { for (int k = 0; k < 60; k++) { if (check(i, j , k)) { cnt ++; } } } } System.out.println(cnt); } public static boolean check(int h, int m, int s) { return h % 10 == 3 || m / 10 == 3 || m % 10 == 3 || s / 10 == 3 || s % 10 == 3; } } - 곱하기 혹은 더하기
import java.io.*; public class Main { public static void main(String[] args) throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); // 곱하기 혹은 더하기 // S의 길이는 1 ~20 // 0~9의 수로 이루어져있음 // 가장 큰 수 구하기 String S = br.readLine(); long ans = S.charAt(0) - '0'; for (int i = 1; i < S.length(); i++) { if (S.charAt(i) - '0' <= 1) { ans += (S.charAt(i) - '0'); } else { ans *= (S.charAt(i) - '0'); } } System.out.println(ans); } } - 좌표 이동하기
import java.util.*; public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); // N을 입력받기 int n = sc.nextInt(); sc.nextLine(); // 버퍼 비우기 String[] plans = sc.nextLine().split(" "); int x = 1, y = 1; // L, R, U, D에 따른 이동 방향 int[] dx = {0, 0, -1, 1}; int[] dy = {-1, 1, 0, 0}; char[] moveTypes = {'L', 'R', 'U', 'D'}; // 이동 계획을 하나씩 확인 for (int i = 0; i < plans.length; i++) { char plan = plans[i].charAt(0); // 이동 후 좌표 구하기 int nx = -1, ny = -1; for (int j = 0; j < 4; j++) { if (plan == moveTypes[j]) { nx = x + dx[j]; ny = y + dy[j]; } } // 공간을 벗어나는 경우 무시 if (nx < 1 || ny < 1 || nx > n || ny > n) continue; // 이동 수행 x = nx; y = ny; } System.out.println(x + " " + y); } }
DFS & BFS
그래프 탐색이란 ?
- 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것
Ex) 특정 도시에서 다른 도시로 갈 수 있는지 없는지, 전자 회로에서 특정 단자와 단자가 서로 연결되어 있는지
- DFS
1. 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사함
2. 즉 넓게(wide) 탐색하기 전에 깊게(deep) 탐색함
3. 모든 노드를 방문하고자 하는 경우에 이 방법을 선택함
4. 깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단함
5. 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느림
깊이 우선 탐색(DFS)의 특징
- 자기 자신을 호출하는 순환 알고리즘의 형태를 지님
- 이 알고리즘을 구현할 때 가장 큰 차이점은 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야한다는 것 (이를 검사하지 않을 경우 무한루프에 빠질 위험이 있음)
깊이 우선 탐색(DFS)의 구현 방법
1. 순환 호출 이용
2. 명시적인 스택 사용

import java.util.ArrayList; /** * DFS 깊이 우선 탐색 * 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘 * 스택 자료구조 (혹은 재귀 함수)를 이용, * 1. 탐색 시작 노드를 스택에 삽입하고 방문 처리 * 2. 스택 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 * 그 노드를 스택에 넣고 방문처리 한다. * 3. 더 이상 2번의 과정을 수행할 수 없을 떄까지 반복 * */ public class DFS { public static boolean[] visited = new boolean[9]; // 방문처리했는지 확인하기 위한 배열 public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>(); // 그래프 전체 // dfs 함수 정의 public static void dfs(int x) { // 현재 노드를 방문 처리 visited[x] = true; System.out.print(x + " "); // 현재 노드와 연결된 다른 노드를 재귀적으로 방문 for (int i = 0; i < graph.get(x).size(); i++) { int y = graph.get(x).get(i); if (!visited[y]) { dfs(y); } } } public static void main(String[] args) { // 그래프 초기화 for (int i = 0; i < 9; i++) { graph.add(new ArrayList<Integer>()); } // 노드 1에 연결된 노드 정보 저장 graph.get(1).add(2); graph.get(1).add(3); graph.get(1).add(8); // 노드 2에 연결된 노드 정보 저장 graph.get(2).add(1); graph.get(2).add(7); // 노드 3에 연결된 노드 정보 저장 graph.get(3).add(1); graph.get(3).add(4); graph.get(3).add(5); // 노드 4에 연결된 노드 정보 저장 graph.get(4).add(3); graph.get(4).add(5); // 노드 5에 연결된 노드 정보 저장 graph.get(5).add(3); graph.get(5).add(4); // 노드 6에 연결된 노드 정보 저장 graph.get(6).add(7); // 노드 7에 연결된 노드 정보 저장 graph.get(7).add(2); graph.get(7).add(6); graph.get(7).add(8); // 노드 8에 연결된 노드 정보 저장 graph.get(8).add(1); graph.get(8).add(7); dfs(1); } }- BFS
1. 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법
2. 즉 깊게(deep) 탐색하기 전에 넓게(wide) 탐색하는 것
3. 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 이 방법을 선택함
너비 우선 탐색(BFS)의 특징
- BFS 는 재귀적으로 동작하지 않는다.
- 이 알고리즘을 구현할 때 가장 큰 차이점은 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야한다는 것이다 이를 검사하지 않을 경우 무한 루프에 빠질 위험이 있다.
- BFS 는 방문한 노드들을 차례로 저장한 후 꺼낼 수 있는 자료 구조인 큐(Queue)를 사용함
- 즉 선입선출(FIFO) 원칙으로 탐색
너비 우선 탐색(BFS)의 구현방법
- 자료구조 큐 (Queue)를 이용
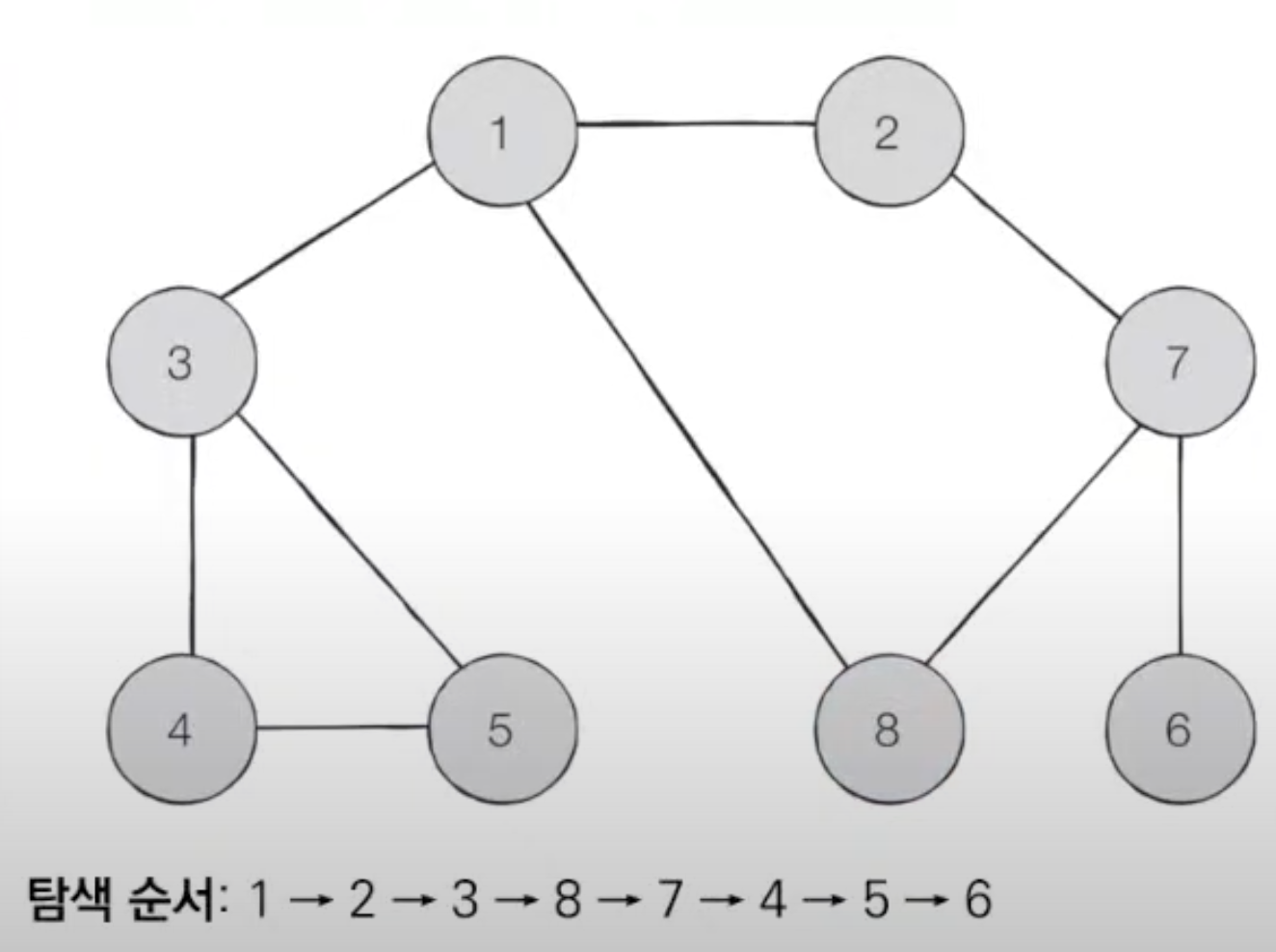
import java.util.ArrayList; import java.util.LinkedList; import java.util.Queue; /** * BFS 너비 우선 탐색 * 그래프에서 가까운 노드부터 우선적으로 탐색하는 알고리즘 * 큐 자료구조 이용, * 1. 탐색 시작 노드를 큐에 삽입하고 방문처리 * 2. 큐에서 노드를 꺼낸 뒤에 해당 노드의 인접 노드 중에서 * 방문하지 않은노드를 모두 큐에 삽입하고 방문 처리한다. * 3. 더 이상 2번의 과정을 수행할 수 없을때까지 반복 */ public class BFS { public static boolean[] visited = new boolean[9]; public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>(); // BFS 함수 정의 public static void bfs(int start) { Queue<Integer> q = new LinkedList<>(); q.offer(start); // 현재 노드를 방문 처리 visited[start] = true; // 큐가 빌 때까지 반복 while (!q.isEmpty()) { // 큐에서 하나의 원소를 뽑아 출력 int x = q.poll(); System.out.print(x + " "); // 해당 원소와 연결된, 아직 방문하지 않은 원소들을 큐에 삽입 for (int i = 0; i < graph.get(x).size(); i++) { int y = graph.get(x).get(i); if (!visited[y]) { q.offer(y); visited[y] = true; } } } } public static void main(String[] args) { // 그래프 초기화 for (int i = 0; i < 9; i++) { graph.add(new ArrayList<Integer>()); } // 노드 1에 연결된 노드 정보 저장 graph.get(1).add(2); graph.get(1).add(3); graph.get(1).add(8); // 노드 2에 연결된 노드 정보 저장 graph.get(2).add(1); graph.get(2).add(7); // 노드 3에 연결된 노드 정보 저장 graph.get(3).add(1); graph.get(3).add(4); graph.get(3).add(5); // 노드 4에 연결된 노드 정보 저장 graph.get(4).add(3); graph.get(4).add(5); // 노드 5에 연결된 노드 정보 저장 graph.get(5).add(3); graph.get(5).add(4); // 노드 6에 연결된 노드 정보 저장 graph.get(6).add(7); // 노드 7에 연결된 노드 정보 저장 graph.get(7).add(2); graph.get(7).add(6); graph.get(7).add(8); // 노드 8에 연결된 노드 정보 저장 graph.get(8).add(1); graph.get(8).add(7); bfs(1); } }- 음료수 채우기
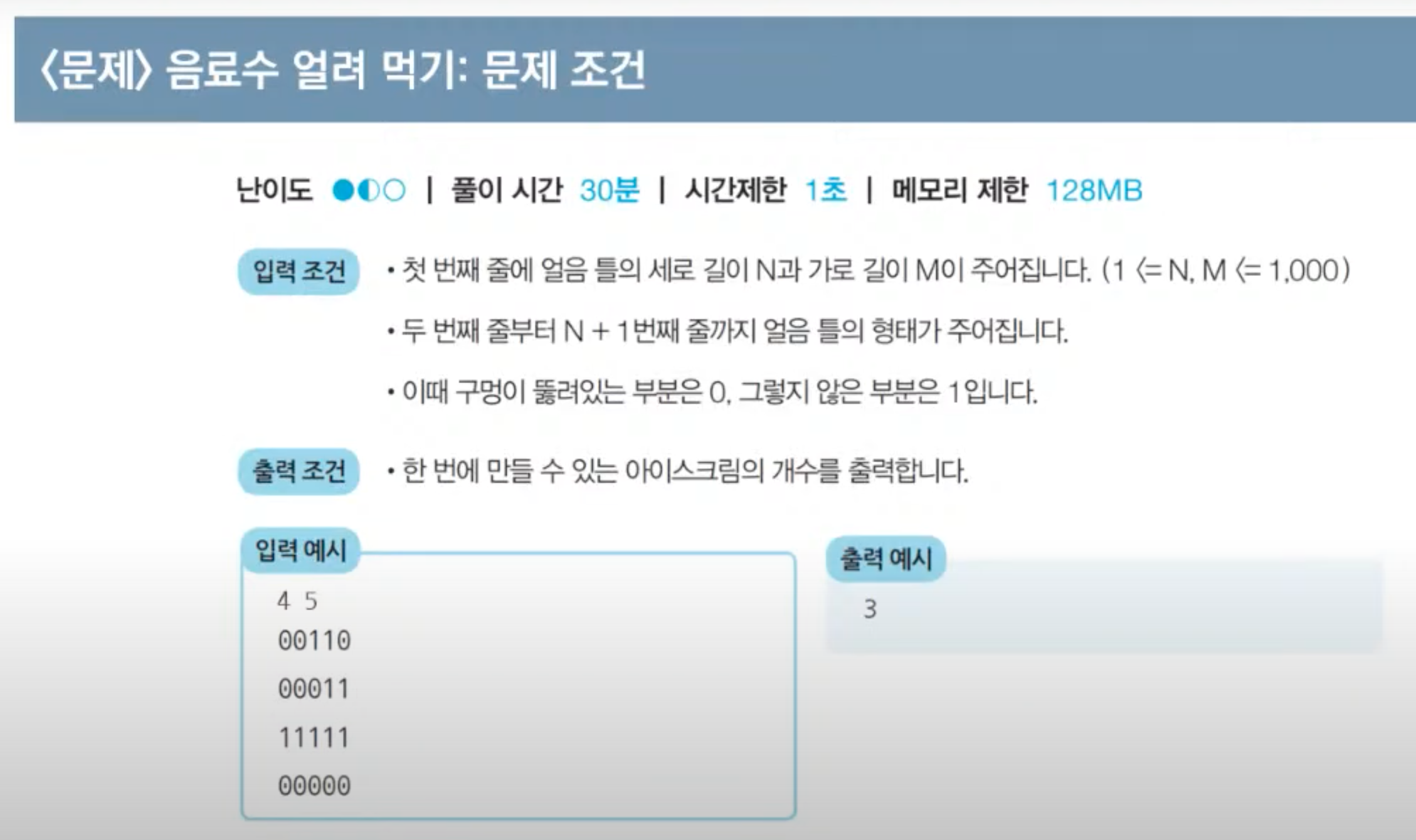
import java.io.*; import java.util.StringTokenizer; /** * 음료수 얼려 먹기 * 첫 번째 줄에 얼음 틀의 세로길이 N, 가로길이 M / N,M : 1~1000 * 두 번째 줄부터 N+1 번째 줄까지 얼음틀의 형태 * 0 : 구멍이 뚫린 부분, 1 : 막힌 부분 * 한 번에 만들 수 있는 아이스크림의 개수 ? */ /** * DFS 활용 * 1. 특정한 지점의 주변의 상, 하, 좌, 우를 살펴본 뒤에 * 주변 지점 중에서 값이 '0'이면서 아직 방문하지 않은 지점이 있다면 해당 지점 방문 * 2. 방문한 지점에서 다시 상, 하, 좌, 우를 살펴보면서 방문을 진행하는 과정을 반복하면, * 연결된 모든 지점을 방문할 수 있다. * 3. 모든 노드에 대하여 1~2 번의 과정을 반복하며, 방문하지 않은 지점의 수를 카운트한다. */ public class Main { public static int n, m; public static int[][] graph = new int[1000][1000]; // dfs로 특정 노드를 방문하고 연결된 모든 노드들도 방문 public static boolean dfs(int x, int y) { // 주어진 범위를 벗어나는 경우에는 즉시 종료 if (x <= -1 || x >= n || y <= -1 || y >= m) { return false; } // 현재 노드를 아직 방문하지 않았다면 if (graph[x][y] == 0) { // 해당 노드 방문 처리 graph[x][y] = 1; // 상, 하, 좌, 우의 위치들도 모두 재귀적으로 호출 dfs(x - 1, y); dfs(x, y-1); dfs(x + 1, y); dfs(x, y + 1); return true; } return false; } public static void main(String[] args) throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); StringTokenizer st = new StringTokenizer(br.readLine()); // n, m 입력 n = Integer.parseInt(st.nextToken()); // 세로 길이 m = Integer.parseInt(st.nextToken()); // 가로 길이 // 2차원 리스트의 맵 정보 입력 받기 for (int i = 0; i < n; i++) { st = new StringTokenizer(br.readLine()); for (int j = 0; j < m; j++) { graph[i][j] = Integer.parseInt(st.nextToken()); } } // 모든 노드(위치)에 대하여 음료수 채우기 int result = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < m; j++) { // 현재 위치에서 dfs 수행 if (dfs(i, j)) { result += 1; } } } System.out.println(result); } }- 미로 탈출

import java.util.LinkedList; import java.util.Queue; import java.util.Scanner; /** * 미로 탈출 * 첫째 줄에 두 정수 N, M 4~200 * 다음 N개의 줄에는 각각 M개의 정수 (0, 1)의 미로 정보가 주어진다. * 또한 시작과 마지막 칸은 항상 1이다. * 괴물이 있는 부분 0, 괴물이 없는 부분 1 * 한 번에 한 칸씩 이동, 시작칸, 마지막칸 포함 * 탈출하기 위해 움직여야 하는 최소 칸의 개수 ? */ class Node { private int index; private int distance; public Node(int index, int distance) { this.index = index; this.distance = distance; } public int getIndex() { return index; } public int getDistance() { return distance; } } public class Main { public static int n, m; public static int[][] graph = new int[201][201]; // 이동할 네 가지 방향 정의 (상, 하, 좌, 우) public static int dx[] = {-1, 1, 0, 0}; public static int dy[] = {0, 0, -1, 1}; public static int bfs(int x, int y) { // 큐 쓰기위해서 queue 라이브러리 사용 Queue<Node> q = new LinkedList<>(); q.offer(new Node(x, y)); // 큐에 노드 넣기 // 큐가 빌 때까지 반복 while (!q.isEmpty()) { Node node = q.poll(); // 꺼내기 x = node.getIndex(); y = node.getDistance(); // 현재 위치에서 4가지 방향으로의 위치 확인 for (int i = 0; i < 4; i++) { int nx = x + dx[i]; int ny = y + dy[i]; // 공간을 벗어난 경우 무시 if (nx < 0 || nx >= n || ny < 0 || ny >= m) { continue; } // 벽인 경우 무시 if (graph[nx][ny] == 0) { continue; } // 해당 노드를 처음 방문하는 경우에만 최단 거리 기록 if (graph[nx][ny] == 1) { graph[nx][ny] = graph[x][y] + 1; q.offer(new Node(nx, ny)); } } } // 가장 오른쪽 아래까지의 최단 거리 반환 return graph[n-1][m-1]; } public static void main(String[] args) { Scanner sc = new Scanner(System.in); // n, m 입력 n = sc.nextInt(); m = sc.nextInt(); sc.nextLine(); // 버퍼지우기 // 맵 정보 입력 받기 for (int i = 0; i < n; i++) { String str = sc.nextLine(); for (int j = 0; j < m; j++) { graph[i][j] = str.charAt(j) - '0'; } } // 결과 출력 System.out.println(bfs(0, 0)); } }
※참조
github.com/ndb796/python-for-coding-test
'Algorithm' 카테고리의 다른 글
다이나믹 프로그래밍 정리 (0) 2020.09.09 트리 정리 (0) 2020.09.07 LinkedList (0) 2020.08.31 EOF (End of File) (0) 2020.08.29 정렬 정리 (0) 2020.08.27